 - from Tianshu Liu, et. al.
- from Tianshu Liu, et. al.
John J. Montgomery, in his manuscript “Discussion on the Various Papers on Soaring Flight.” Proceedings of the International Conference on Aerial Navigation. Chicago, August 1-4. 1893 observed that:
“In the examination of the wings of hawks, buzzards, eagles, sea gulls, pelicans, wild geese, and other birds, I found the under surface of the wing from the front to the rear edge a true parabola, varying in its curvature, both according to the relation between the weight of the bird and its wing surface and the proportion of length and breadth of the wing. A comparison between these various models suggests that the curvature is also affected by the tilt given the wings from the base to the tip.
“The parabolic curvature a few inches from the base of the wing seems most perfect. At this point the front edge is the vertex of the parabola.
“In comparing the distance between the front and rear edges—the chord—with the focal length of the parabolic curve, the following order seems to exist. The length of the cord is to the focal length as the weight of the bird is to the wing surface; this relation being affected by the proportion between the length and breadth and the tilt of the wings. I do not give this as an exact proportion, but simply as an indication of the relations. In the pelican’s wing the chord is five or six times the focal length of the curve; in the gull’s it is three or four times, while in hawks and buzzards it is two or three times.”
Montgomery’s Conjecture:
C/F ~ W/A
where
C = Mean Chord Length = A/L
F = Focal Length
W = Weight
A = Area of wing surface
L = Length of wing
with
Pelicans: C/F ~ 5–6 x W/A
Gulls: C/F ~ 3–4 x W/A
Hawks & Buzzards: C/F ~ 2–3 x W/A
Are bird's wings parabolic in shape as Montgomery observed?
There are few useable images or measurements of bird's wings in profile in the available literature. The exception is a 2004 AIAA paper by Tianshu Liu, et. al. [ref].
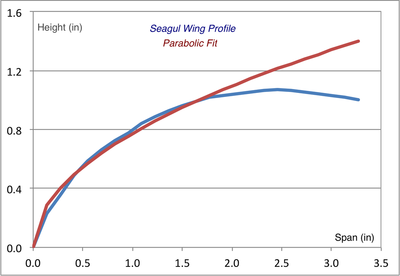
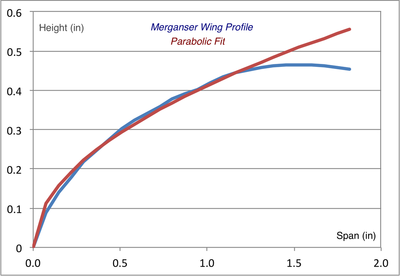
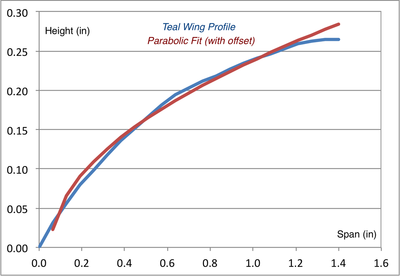
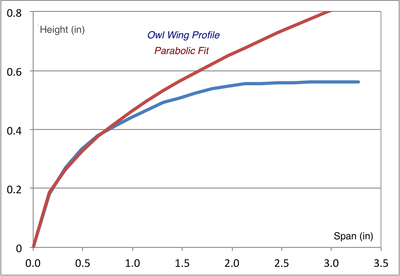
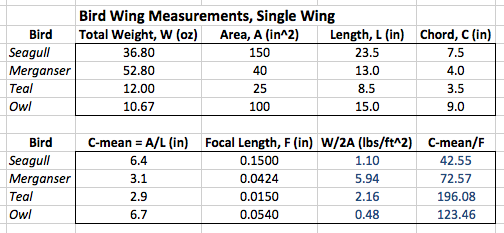
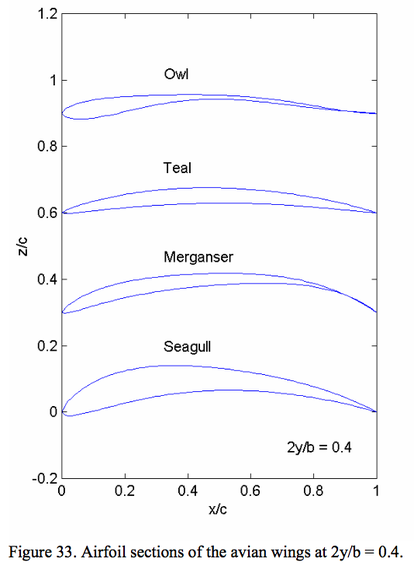
Shown above is a figure from their paper comparing a Seagull's, Merganser's, Teal's and Owl's wings, normalized to the chord length, c. They employed "non-contact surface measurements using a three-dimensional laser scanner ... that is accurate to 0.041 mm."
We digitized their data and found that, near the leading edge, these wings are close to being parabolic in shape. The fits to these wings are shown below, indicating that, within the first inch or two of the front edge, they are very close to parabolic. To obtain a good fit it was necessary to add an offset (0.055") to the Teal's wing:
__________________________________________________________
[ref] Tianshu Liu, K. Kuykendoll, R. Rhew, and S. Jones, "Avian Wings," 24th AIAA Aerodynamic Measurement Technology and Ground Testing Conference, 28 June–1 July, 2004, AIAA 2004-2186. view
“In the examination of the wings of hawks, buzzards, eagles, sea gulls, pelicans, wild geese, and other birds, I found the under surface of the wing from the front to the rear edge a true parabola, varying in its curvature, both according to the relation between the weight of the bird and its wing surface and the proportion of length and breadth of the wing. A comparison between these various models suggests that the curvature is also affected by the tilt given the wings from the base to the tip.
“The parabolic curvature a few inches from the base of the wing seems most perfect. At this point the front edge is the vertex of the parabola.
“In comparing the distance between the front and rear edges—the chord—with the focal length of the parabolic curve, the following order seems to exist. The length of the cord is to the focal length as the weight of the bird is to the wing surface; this relation being affected by the proportion between the length and breadth and the tilt of the wings. I do not give this as an exact proportion, but simply as an indication of the relations. In the pelican’s wing the chord is five or six times the focal length of the curve; in the gull’s it is three or four times, while in hawks and buzzards it is two or three times.”
Montgomery’s Conjecture:
C/F ~ W/A
where
C = Mean Chord Length = A/L
F = Focal Length
W = Weight
A = Area of wing surface
L = Length of wing
with
Pelicans: C/F ~ 5–6 x W/A
Gulls: C/F ~ 3–4 x W/A
Hawks & Buzzards: C/F ~ 2–3 x W/A
Are bird's wings parabolic in shape as Montgomery observed?
There are few useable images or measurements of bird's wings in profile in the available literature. The exception is a 2004 AIAA paper by Tianshu Liu, et. al. [ref].
Shown above is a figure from their paper comparing a Seagull's, Merganser's, Teal's and Owl's wings, normalized to the chord length, c. They employed "non-contact surface measurements using a three-dimensional laser scanner ... that is accurate to 0.041 mm."
We digitized their data and found that, near the leading edge, these wings are close to being parabolic in shape. The fits to these wings are shown below, indicating that, within the first inch or two of the front edge, they are very close to parabolic. To obtain a good fit it was necessary to add an offset (0.055") to the Teal's wing:
__________________________________________________________
[ref] Tianshu Liu, K. Kuykendoll, R. Rhew, and S. Jones, "Avian Wings," 24th AIAA Aerodynamic Measurement Technology and Ground Testing Conference, 28 June–1 July, 2004, AIAA 2004-2186. view
All figures from Tianshu Liu, et. al.
Montgomery's Conjecture that C/F ~ W/A
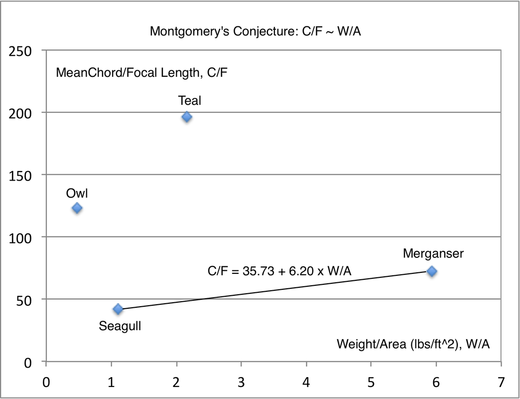
These results indicate that C/F does increase with W/A, consistent with Montgomery's conjecture.
Seagull and Merganser, having similar wings, show that C/F ~ 6.20 x W/A, consistent with what Montgomery observed for Pelicans: C/F ~ 5–6 x W/A. Owl and Teal, with dissimilar wings, should probably not be grouped together.
More data on more birds is required to completely verify Montgomery's conjecture.
Tianshu Liu, et. al. provide the reason for the lack of data on bird's wing and surmise that more information may be available in the future:
"Inspired by bird flight, early aviation researchers have studied avian wings as the basics of developing man-made flight vehicles. … This may be partially the reason why early aircraft designers ... tended to use thin airfoils by simply simulating bird wings. (T)his situation was dramatically changed since thick airfoils … achieved much higher lift-to-drag ratio at Reynolds numbers in airplane flight. Thus, study of avian wings becomes a marginalized topic that only interests a few avian biologists and zoologists. … Recently, there is renewed interest in low-Reynolds- number flight and flapping flight in the aerospace community due to the need of developing micro-air-vehicles (MAVs). Hence, it is worthwhile to revisit the problem of the geometry and aerodynamics of avian wings."
Seagull and Merganser, having similar wings, show that C/F ~ 6.20 x W/A, consistent with what Montgomery observed for Pelicans: C/F ~ 5–6 x W/A. Owl and Teal, with dissimilar wings, should probably not be grouped together.
More data on more birds is required to completely verify Montgomery's conjecture.
Tianshu Liu, et. al. provide the reason for the lack of data on bird's wing and surmise that more information may be available in the future:
"Inspired by bird flight, early aviation researchers have studied avian wings as the basics of developing man-made flight vehicles. … This may be partially the reason why early aircraft designers ... tended to use thin airfoils by simply simulating bird wings. (T)his situation was dramatically changed since thick airfoils … achieved much higher lift-to-drag ratio at Reynolds numbers in airplane flight. Thus, study of avian wings becomes a marginalized topic that only interests a few avian biologists and zoologists. … Recently, there is renewed interest in low-Reynolds- number flight and flapping flight in the aerospace community due to the need of developing micro-air-vehicles (MAVs). Hence, it is worthwhile to revisit the problem of the geometry and aerodynamics of avian wings."
Montgomery's Santa Clara Wing
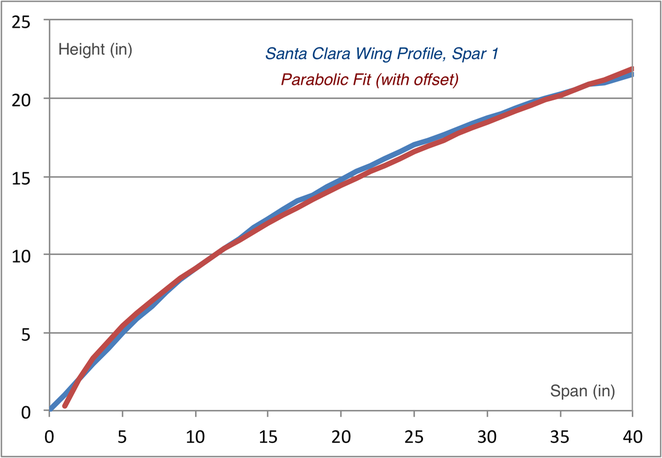
Montgomery's Santa Clara Wing is parabolic over its entire span, with 3.4" chopped off the front edge.
It has a Chord of 40" and a Focal Length of 4.0", so that C/F = 40/4 = 10 and W/A = 190/144 = 1.32 lbs/ft^2 (with pilot).
It has a Chord of 40" and a Focal Length of 4.0", so that C/F = 40/4 = 10 and W/A = 190/144 = 1.32 lbs/ft^2 (with pilot).